Imprimer tout le livreImprimer tout le livre

5.2 : La mesure des inégalités

Site: ZERUN
Cours: Macroéconomie 1
Livre: 5.2 : La mesure des inégalités
Imprimé par: Visiteur anonyme
Date: jeudi 21 novembre 2024, 19:02

Table des matières

1. Des inégalités de quoi ?

Il peut exister de multiples inégalités : de salaire, de revenu, de richesse, mais aussi d’accès aux soins, à l’éducation, etc. Si l’ensemble de ces inégalités sont susceptibles d’intéresser les économistes (qui cherchent à les comprendre, ou à étudier leurs conséquences), nous allons ici nous limiter aux inégalités de revenu et de richesse qui sont celles les plus étudiées en macroéconomie.

Encore une fois, il faut distinguer les deux. Les revenus sont des flux ; c’est ce qu’une personne gagne durant une période donnée. A l’inverse, la richesse est un stock. C’est le montant qu’une personne détient sur son compte en banque plus la valeur de sa maison, par exemple.

On peut reprendre la métaphore de la baignoire se remplissant peu à peu d’eau : ce qui coule du robinet est un flux (ici, le revenu) et le liquide au fond de la baignoire est un stock (ici, la richesse). Cette distinction a une importance quand on discute d’inégalités. En effet, du fait de l’accumulation de richesse au cours du temps (le « stock » de richesse étant irrigué par le « flux » des revenus), les inégalités de richesse sont généralement largement plus importantes que celles de revenus.

2. Une première mesure

Une fois cette clarification apportée, qu'en est-il du niveau d’égalité ou d’inégalité de nos sociétés ?

On peut facilement se rendre compte qu’il existe des inégalités de revenus. Par exemple, en 2018, la rémunération moyenne des patrons du CAC40 atteignait 5,77 millions d’euros soit environ 277 fois le salaire minimum en France (et 152 fois le salaire moyen) [1]. De même, on peut facilement constater des écarts de richesse. Ainsi, en 2016 l’ONG Oxfam estimait que les 62 personnes les plus riches au monde détenaient autant que les 50% les plus pauvres et par ailleurs, que les 1% les plus riches sur la planète possédaient plus que les 99% restant de la population mondiale.[2] Ces chiffres sont parlants et mobilisateurs – ils sont d’ailleurs à l’origine du slogan « nous sommes les 99% » lors de mouvements sociaux comme le mouvement Occupy (Wall Street, puis d'autres lieux) - mais peuvent-ils constituer une mesure des inégalités dans une société ? Fournissent-ils une statistique suffisante afin de comparer deux sociétés ou d’étudier l’évolution des inégalités dans une société ? Du moins, comment les comprendre ?

Une manifestation avec des gens brandissant des pancartes.

Pour mesurer les inégalités au sein d’une société, on peut utiliser la part de la richesse (ou du revenu) possédée par les individus les plus fortunés (souvent les 1% ou les 10%). Ces variables sont généralement sensibles aux politiques publiques affectant les inégalités de revenu et de richesse et peuvent donc nous donner une information si celles-ci augmentent ou au contraire diminuent. Par ailleurs, lorsque l’on souhaite mesurer les évolutions sur le long terme, on est parfois contraint d’utiliser cette mesure. En effet, les sources historiques sur les individus les plus fortunés sont souvent largement plus nombreuses et plus faciles d’accès que sur le restant de la population: en occident, les plus riches (rois, grands nobles, ecclésiastiques, etc.) avaient souvent des biographes et des archives, facilitant ainsi la mesure de leurs patrimoines et de leurs revenus. On peut parfois également obtenir des estimations du revenu ou de la richesse totale au sein d'une économie. On peut ainsi estimer "la part des plus aisés" quand d'autres indicateurs sont plus difficiles à obtenir.

Remarque : Thomas Piketty (économiste, né en 1971) dans ses nombreux ouvrages consacrés aux inégalités ou aux hauts patrimoines utilise régulièrement les revenus ou salaire des 1% ou 10% les plus fortunés. Le lien suivant conduit vers un des graphiques de son ouvrage Le Capital au 21ème siècle (2013) où il montre les évolutions de la part du décile supérieur dans le revenu national (la part des 10% des individus ayant les revenus les plus élevés) : http://piketty.pse.ens.fr/files/capital21c/pdf/G8.1.pdf

  •  Une première mesure des inégalités de revenus est donc la part des 1% des revenus les plus élevés dans l’ensemble des revenus générés par une société.
    \( I_{rev} = \frac{Revenus des 1\% avec les plus hauts revenus}{Revenus totaux} \)
    On peut procéder de même avec les 10% plus hauts revenus plutôt que les 1%.

  •  Une première mesure des inégalités de richesse est donc la part des 1% des plus hautes fortunes dans l’ensemble de la richesse d’un pays.
    \( I_{richesse} = \frac{Richesse des 1\% les plus fortunés}{Richesse totale} \)
    On peut procéder de même avec les 10% les plus riches plutôt que les 1%.

 

Toutefois, il ne faut pas oublier les limites de cette méthode. Se focaliser sur les 1% les plus riches (ou les 10% les plus riches) oublie justement de mesurer les évolutions des inégalités dans les 99% (ou 90%) restants. Il peut pourtant y avoir de grande disparité au sein de cette partie de la population et ces disparités peuvent largement changer dans le temps. C’est pourquoi les économistes ne se contentent pas de cette mesure des inégalités et multiplient les méthodes afin de mesurer et comparer le niveau d’inégalités dans une société.


[1] En général, lorsque l'on parle de revenu et de richesse on préfèrera utiliser la "médiane" plutôt que la moyenne. Cette dernière est en effet sensible à la présence de valeur extrême (des individus très riches). Toutefois, selon les sources, les valeurs médianes ne sont pas toujours disponibles.
https://www.lemonde.fr/economie/article/2019/11/07/les-pdg-du-cac-40-ont-gagne-en-moyenne-277-fois-le-smic-en-2018_6018344_3234.html

[2] Il faut parfois faire attention au mode de calcul derrière ces chiffres. La personne la plus « pauvre » au monde pourrait être une personne vivant tout à fait convenablement mais ayant emprunté de l’argent, la conduisant à avoir une richesse négative (des dettes). Ces éléments "techniques" dans les calculs ne doivent toutefois pas faire oublier les écarts de richesses manifestes soulignés par ces indicateurs.
Autrement, le chiffre peut être retrouvé dans cet article de presse :
Inégalités : les 1 % les plus riches du monde possèdent plus que le reste de la planète, Les Echos, 18 janvier 2016.
https://www.lesechos.fr/2016/01/inegalites-les-1-les-plus-riches-du-monde-possedent-plus-que-le-reste-de-la-planete-194738


3. L’indice de Gini

Un des indicateurs les plus couramment employé par les économistes afin de mesurer les inégalités est l’indice de Gini (appelé ainsi en l’honneur du statisticien Corrado Gini qui a « inventé » cet indice).

Voici sa définition selon l’INSEE :

L'indice (ou coefficient) de Gini est un indicateur synthétique permettant de rendre compte du niveau d'inégalité pour une variable et sur une population donnée. Il varie entre 0 (égalité parfaite) et 1 (inégalité extrême). Entre 0 et 1, l'inégalité est d'autant plus forte que l'indice de Gini est élevé.

Il est égal à 0 dans une situation d'égalité parfaite où la variable prend une valeur identique sur l’ensemble de la population. À l'autre extrême, il est égal à 1 dans la situation la plus inégalitaire possible, où la variable vaut 0 sur toute la population à l’exception d’un seul individu.

Les inégalités ainsi mesurées peuvent porter sur des variables de revenus, de salaires, de niveau de vie, etc.

Source INSEE : https://www.insee.fr/fr/metadonnees/definition/c1551

L’indice de Gini est donc un indicateur synthétique d’inégalité. C’est-à-dire que l’on s’intéresse aux inégalités et que nous allons créer un indicateur (un nombre) qui résume des informations à propos de ces inégalités (un peu comme votre moyenne en mathématiques résume les informations sur les notes en mathématiques que vous avez obtenus). Mais de quelles informations parle-t-on exactement ? Dans le cas qui nous préoccupe aujourd’hui – les inégalités de revenu et de richesse – on va s’intéresser à la distribution entière du revenu ou de la richesse de la population.

Une remarque : puisque l’on va s’intéresser initialement à la distribution entière du revenu/de la richesse, il faut normalement pouvoir observer cette distribution entière. Pour la première mesure évoquée – la part des 1% (ou 10%) les plus fortunés dans le revenu (ou la richesse) totale d’un pays – on avait simplement besoin de la richesse du groupe considérée (les 1 ou 10% les plus aisés) ainsi qu'une information sur la richesse totale (et cette dernière peut parfois être estimée indirectement). Pour l'indice de Gini, il faut maintenant une information bien plus précise : les revenus (ou la richesse) de l’ensemble de la population. En pratique, on utilise souvent une approximation assez fine de cette distribution basée sur les centiles ou les déciles.


4. Méthode de calcul

Comment procède-t-on en pratique pour calculer l’indice de Gini ?

Il est plus facile de présenter cet indice en partant d’un exemple. Aussi, imaginons une société composée de 10 individus. Chaque individu possède une richesse (ou un revenu).

Nous allons maintenant effectuer les opérations suivantes :
(1)     Calculer la richesse totale.
(2)     Classer les individus par ordre de revenu/richesse croissant. En cas d’égalité entre deux individus, l’ordre entre ces deux individus importe peu.
(3)     Calculer la part de chaque individu dans la richesse totale.
(4)     Calculer la part cumulée des X individus (ou X% des individus) les plus pauvres dans la richesse totale.
(5)     Tracer dans un repère la courbe qui indique la part de richesse des X% les individus les plus pauvres. Cette courbe est appelée la courbe de Lorentz.
(6)     Calculer l’aire sous la courbe de Lorentz, appelons-la « B ».
(7)    Le coefficient de Gini est calculé avec la formule suivante : \( Gini = 1-2B \).

5. Gini - Illustration 1

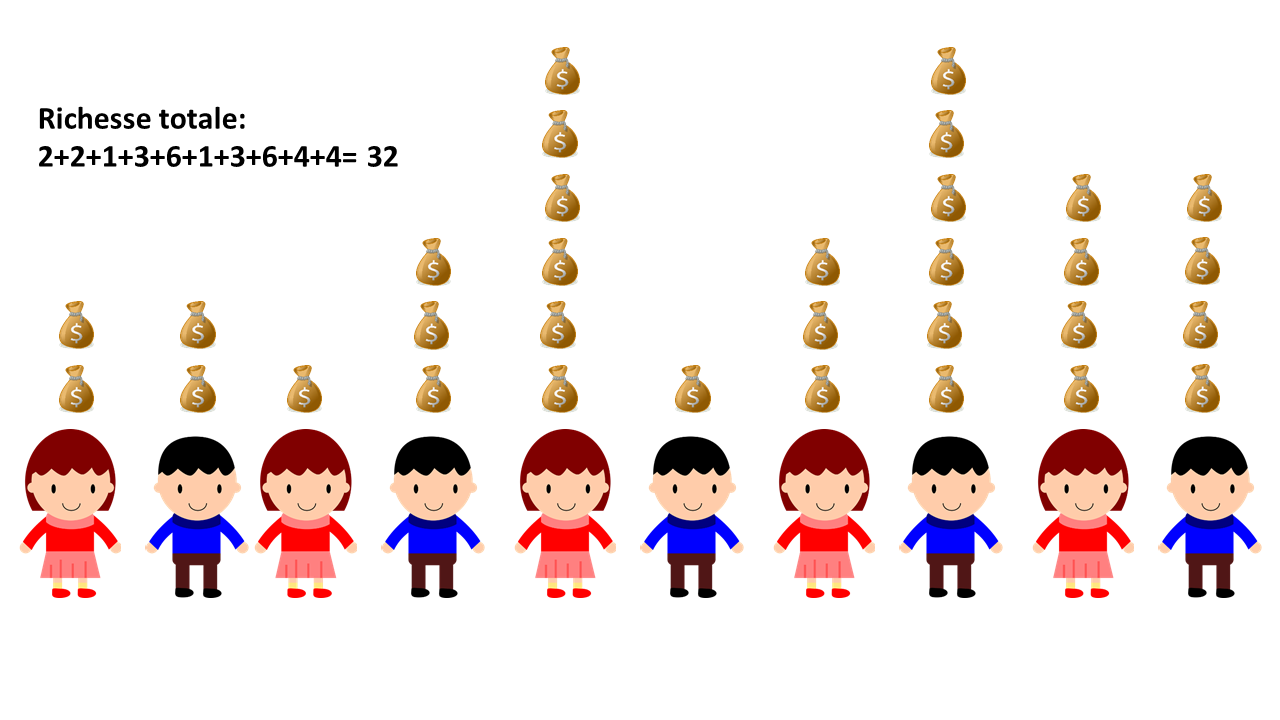
Voici la population de départ. Elle est composée de 10 individus possédant chacun une richesse symbolisée par des bourses.

La répartition inégale de la richesse dans une population : 10 personnages avec chacun un nombre différent de sacs d'argent


On calcule la richesse totale (qui vaut 32) :

Calcul de la richesse totale en additionnant le nombre de bourses d'argent 2+2+1+3+6+1+3+6+4+4=32


6. Gini - Illustration 2

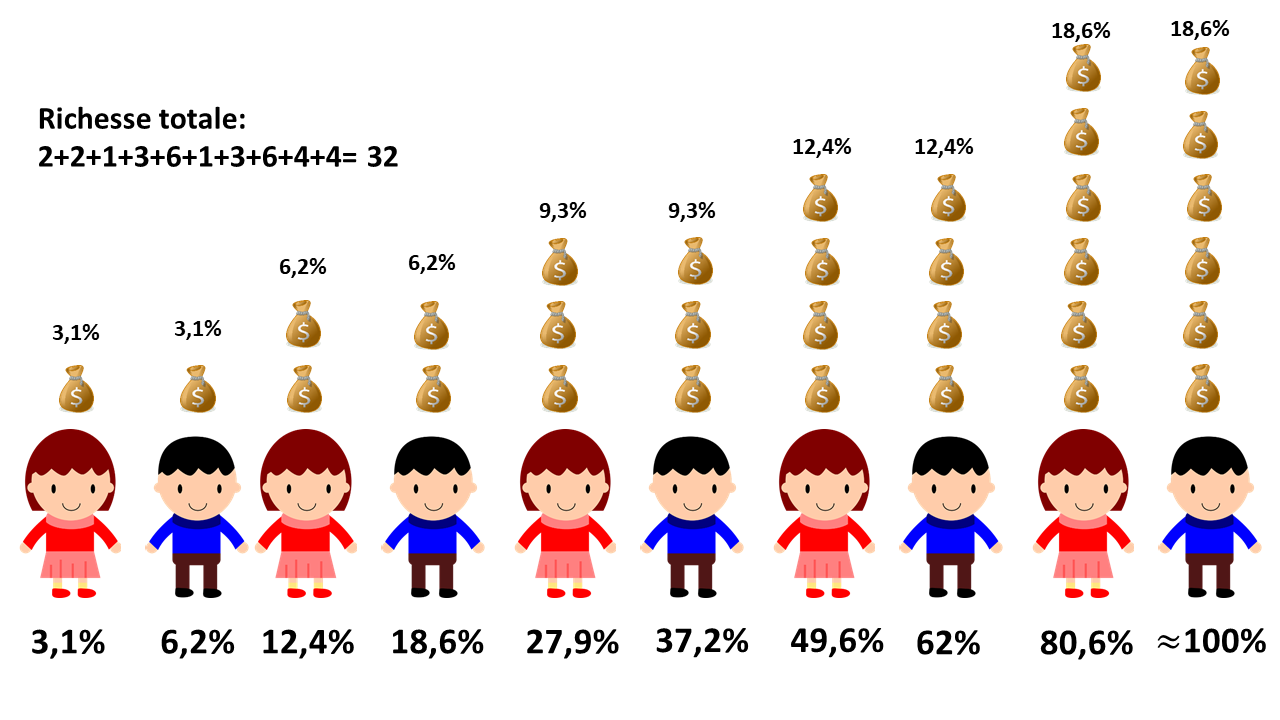
On classe la population par ordre croissant de richesse :

L'individu avec le moins de bourses d'argent est placé à gauche, celui avec le plus de bourses à droiteOn calcule la part de chacun dans la richesse totale, puis la richesse totale cumulée par les X% les plus pauvres.
Ici comme nous avons 10 individus, 1 personne = 10% de la population totale.

Part de richesse exprimé en pourcentage du total, de 3,1% à droite jusqu’à 18,6% à gauche


7. Gini - Illustration 3

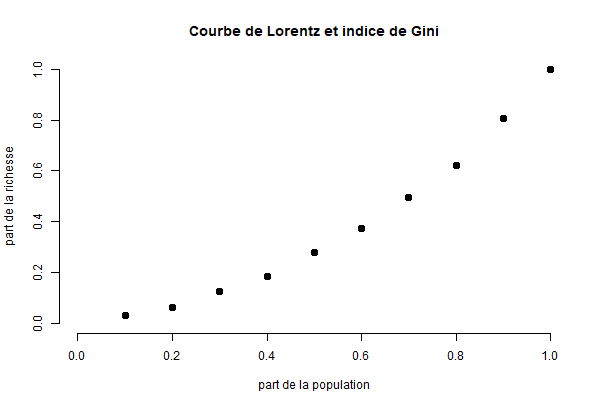
On trace ensuite dans un repère la courbe qui indique le % de richesse détenu par les X% les plus pauvres. Pour ce faire, on trace d’abord les points indiquant les pourcentages calculés précédemment.

Par exemple, mon premier point va se situer en x= 0.1 (indiquant que la première personne correspond au 10% les plus pauvres) et y = 0.031 (cette personne possède 3.1% de la richesse totale). On va ensuite tracer le point x=0.2 et y = 0.0662, puis le point x=0.3, y=0.124, etc. jusqu’au point x=1, y=1.

Graphique avec une série de points allant de x = 0.1, y = 0.031 jusqu'à x=1, y=1

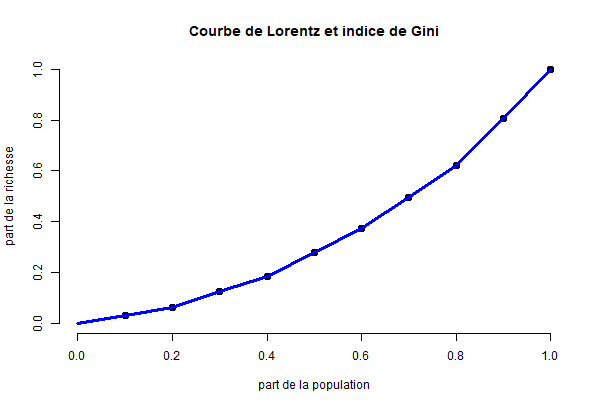
On relie ensuite ces points et on obtient la courbe de Lorentz en bleu dans le graphique suivant.

On relie ensuite ces points et on obtient la courbe de Lorentz en bleu dans le graphique.

8. Gini - Illustration 4

On peut maintenant calculer l’indice de Gini en calculant l’aire sous cette courbe bleu (appelons-la « B ») et en appliquant la formule : Gini = 1-2B.

Pour mieux comprendre ce que l’on regarde, on peut imaginer une société parfaitement égalitaire. Si on traçait la courbe de Lorentz pour cette société, on obtiendrait simplement un segment reliant les points (0,0) et (1,1). En effet, dans cette société les 10% les « plus pauvres » possèdent 10% de la richesse, les 20% les "plus pauvres" possèdent 20% de la richesse, etc. En traçant la courbe de Lorentz dans cette société, on obtient la courbe rouge.

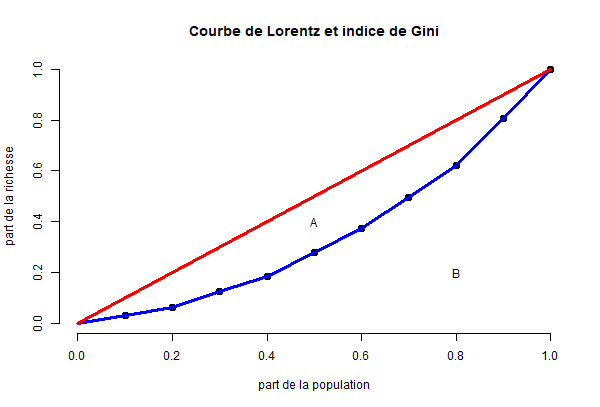
L’indice de Gini = l’aire sous cette courbe bleu. La courbe rouge montre l'hypothèse d'une société égalitaire

On peut alors définir deux zones : A et B.

L’indice de Gini est égal à "1-2B". C'est en fait une mesure de l'éloignement entre les courbes rouge et bleue. Plus la courbe bleue se rapproche de la courbe rouge (et donc de l’égalité parfaite), plus la zone B est importante. Aussi, l’indice de Gini (1-2B) va se rapprocher de 0. A l’inverse, plus la société est inégalitaire, plus la courbe bleue va s’éloigner de la courbe rouge. L’aire « B » sera petite et l’indice de Gini (1-2B) va être important.

En résumé :

  • Plus on s’approche de 1 plus les inégalités sont fortes.
  • Plus on s’approche de 0, plus on s’approche de l’égalité parfaite.


Remarque :
On calcule l’indice de Gini comme "1-2B". Il est aussi égal à 2A. Il s’agit d’un simple calcul géométrique. L’aire sous la courbe rouge vaut 1/2 : C’est un triangle rectangle de longueur 1 et de hauteur 1.
L’air « A » est égale à l’aire globale moins l’aire de « B » : A = ½ - B.
Le coefficient de Gini est égal à 1-2B ; c’est donc deux fois l’air de A.


9. Rappel de géométrie

L'indice de Gini demande de calculer des aires.

On peut calculer l’indice de Gini avec des aires de triangles et de trapèzes.
L’aire d’un triangle vaut : base X hauteur X ½
L’aire d’un trapèze vaut : (petite base + grande base) X hauteur X ½

Par exemple, dans l'illustration précédente, il faudrait calculer l'aire sous la courbe bleue. Or, on peut découper cette aire en un ensemble de triangles et de trapèzes:

Découpage de l'aire sous la courbe bleue en un ensemble de triangles et de trapèzes

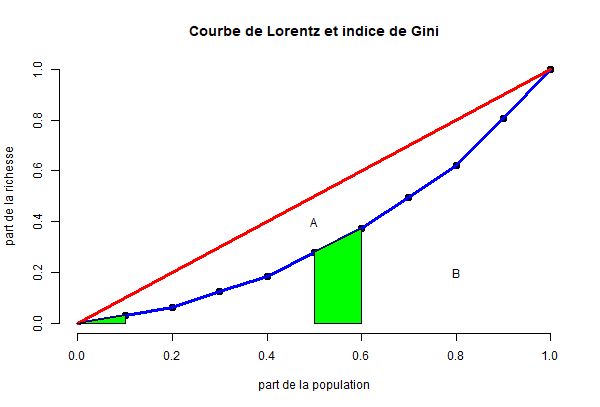
10. Gini - un exemple simple

Pour ne pas s’embarquer dans un calcul trop long, imaginons une société avec trois groupes d’individus de même taille (33.3% de la population chacun).

-        Les plus pauvres ne possèdent rien.

-        Le groupe intermédiaire possède 25% de la richesse totale.

-        Le groupe le plus riche possède 75% de la richesse totale.

On peut tracer la courbe de Lorentz comme suit :

-        Le point x=0.333, y = 0

-        Le point x=0.666, y = 0.25

-        Le point x=1, y = 1

On obtient la courbe de Lorentz et on va s’intéresser à l’aire de « B ».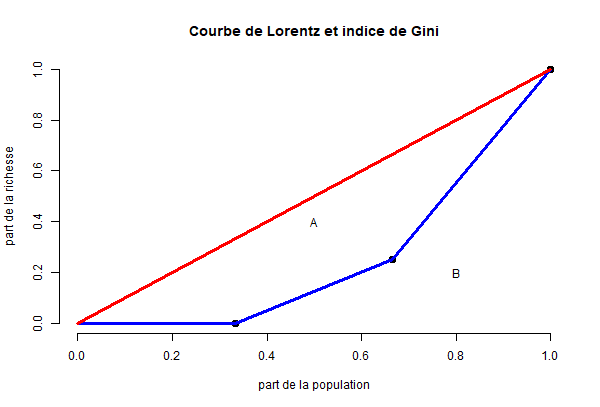
Trace de la courbe de Lorentz où le point x=0.333, y = 0, le point x=0.666, y = 0.25, le point x=1, y = 1

On remarque qu’on peut la calculer facilement en calculant l’aire du triangle vert et du trapèze jaune.

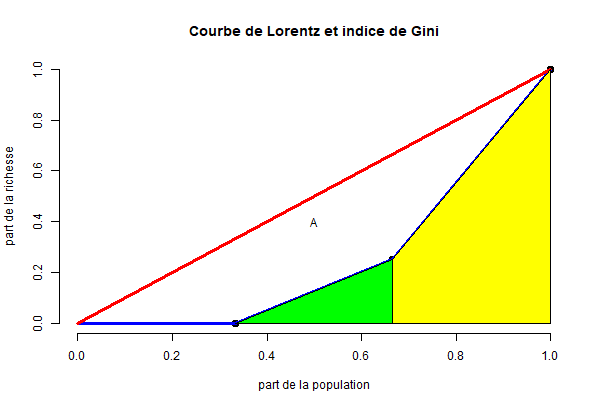
Illustration de l'aire vert et de l'aire jaune

Le triangle vert :
Base = 0.333
Hauteur = 0.25
On obtient : Aire = 0.042

Le trapèze :
Petite base = 0.25
Grande base = 1
Hauteur = 0.333
On obtient : Aire = 0.21

Gini:
L’aire de B vaut donc : 0.042+0.21 = 0.252
L’indice de Gini vaut donc : 1-2B = 0.496




11. Gini en France

Il existe d’autres mesures des inégalités de richesse ou de revenu, mais l’indice de Gini reste un classique. Le lien suivant conduit vers un graphique de l’INSEE où l’indice de Gini sur « le niveau de vie » est tracé pour la France : https://www.insee.fr/fr/statistiques/2491918#graphique-figure1


Le niveau de vie se définit ainsi :
Le niveau de vie est égal au revenu disponible du ménage divisé par le nombre d'unités de consommation (uc). Le niveau de vie est donc le même pour tous les individus d'un même ménage.
Les unités de consommation sont généralement calculées selon l'échelle d'équivalence dite de l'OCDE modifiée qui attribue 1 uc au premier adulte du ménage, 0,5 uc aux autres personnes de 14 ans ou plus et 0,3 uc aux enfants de moins de 14 ans.
Source INSEE : https://www.insee.fr/fr/metadonnees/definition/c1890

Le niveau de vie est donc calculé à partir du revenu des ménages. On calcule le revenu total des personnes vivant dans un même foyer et on le divise par un nombre qui dépend du nombre de personnes vivant dans ce foyer.

Ce que l’on peut constater, c’est que l’indice de Gini mesurant ces inégalités de « niveau de vie », après avoir diminué jusqu’à la fin des années 90 semble maintenant remonter. Ainsi, les inégalités de niveau de vie, après avoir baissé au cours du XXème siècle, semblent repartir à la hausse depuis une vingtaine d’années.


12. Le rapport inter décile

Une dernière remarque : Il existe d’autres mesures des inégalités qui ont chacune leurs avantages et leurs inconvénients : par exemple, les rapports inter déciles, les indices d’Atkinson, etc.

Si les indices d’Atkinson sont assez complexes, le rapport inter décile est en revanche assez intuitif et couramment employé.

Généralement, on va le calculer sur le revenu (ou la richesse) en utilisant le 1er et le 9ème décile de la distribution de revenu. Cela signifie que l’on regarde :

-        Le revenu de la personne telle que 10% de la population a un revenu inférieur (le premier décile).

-        Le revenu de la personne telle que 90% de la population a un revenu inférieur (le 9ème décile).

Puis ont fait simplement le rapport entre ces deux revenus.

Intuitivement, on va créer deux groupes : « les 10% les plus pauvres » et « les 10% les plus riches » et regarder combien de fois le « plus pauvre des riches » va gagner le revenu du « plus riche des pauvres ».

\( I_{\frac{D9}{D1}} = \frac{D9}{D1} \) où \(D1\) et \(D9\) sont les premier et 9ème décile de la distribution de revenu.

Graphique

L’évolution du rapport inter-décile semble confirmer ce qu’on a observé plus tôt avec le coefficient de Gini : il semble avoir baissé avec un minimum vers 2004, puis il semble ré-augmenter légèrement.